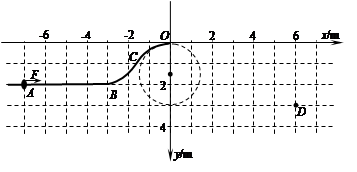(16分)在竖直平面内固定一轨道ABCO, AB段水平放置,长为4 m,BCO段弯曲且光滑,轨道在O点的曲率半径为1.5 m;一质量为1.0 kg、可视作质点的圆环套在轨道上,圆环与轨道AB段间的动摩擦因数为0.5。建立如图所示的直角坐标系,圆环在沿x轴正方向的恒力F作用下,从A(-7,2)点由静止开始运动,到达原点O时撤去恒力F,水平飞出后经过D(6,3)点。重力加速度g取10m/s2,不计空气阻力。求:
⑴圆环到达O点时对轨道的压力;
⑵恒力F的大小;
⑶圆环在AB段运动的时间。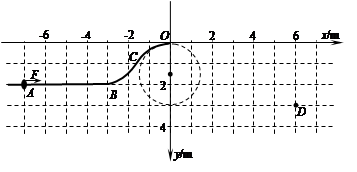
(16分)在竖直平面内固定一轨道ABCO, AB段水平放置,长为4 m,BCO段弯曲且光滑,轨道在O点的曲率半径为1.5 m;一质量为1.0 kg、可视作质点的圆环套在轨道上,圆环与轨道AB段间的动摩擦因数为0.5。建立如图所示的直角坐标系,圆环在沿x轴正方向的恒力F作用下,从A(-7,2)点由静止开始运动,到达原点O时撤去恒力F,水平飞出后经过D(6,3)点。重力加速度g取10m/s2,不计空气阻力。求:
⑴圆环到达O点时对轨道的压力;
⑵恒力F的大小;
⑶圆环在AB段运动的时间。