(14分)如图所示，一儿童玩具静止在水平地面上，一个幼儿沿与水平面成53°角的恒力拉着它沿水平面运动，已知拉力F＝4.0N，玩具的质量m＝0.5kg，经过时间t＝2.0s，玩具移动了距离x＝4.8m，这时幼儿松开手，玩具又滑行了一段距离后停下．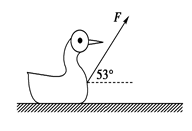
(1)全过程玩具的最大速度是多大？
(2)松开手后玩具还能运动多远？
(取g＝10m/s2.sin53°＝0.8，cos53°＝0.6)
如图所示，双星系统中的星球A、B都可视为质点，A、B绕两者连线上的O点做匀速圆周运动，A、B之间距离不变，引力常量为G，观测到A的速率为v、运行周期为T，A、B的质量分别为mA、mB．
（1）求B的周期和速率．
（2）A受B的引力FA可等效为位于O点处质量为m′的星体对它的引力，试求m′．（用mA、mB表示）（ ）
光滑圆轨道和两倾斜直轨道组成如图所示装置，其中直轨道bc粗糙，直轨道cd光滑，两轨道相接处为一很小的圆弧．质量为m=0.1kg的滑块（可视为质点）在圆轨道上做圆周运动，到达轨道最高点a时的速度大小为v=4m/s，当滑块运动到圆轨道与直轨道bc的相切处b时，脱离圆轨道开始沿倾斜直轨道bc滑行，到达轨道cd上的d点时速度为零．若滑块变换轨道瞬间的能量损失可忽略不计，已知圆轨道的半径为R=0.25m，直轨道bc的倾角θ=37°，其长度为L=26.25m，d点与水平地面间的高度差为h=0.2m，取重力加速度g=10m/s2，sin37°=0.6．求：
（1）滑块在圆轨道最高点a时对轨道的压力大小；
（2）滑块与直轨道bc问的动摩擦因数；
（3）滑块在直轨道bc上能够运动的时间．
由于地球自转的影响，地球表面的重力加速度会随纬度的变化而有所不同：若地球表面两极处的重力加速度大小为g0，在赤道处的重力加速度大小为g，地球自转的周期为r，引力常量为G，地球可视为质量均匀分布的球体．求：
（1）地球半径R；
（2）地球的平均密度；
（3）若地球自转速度加快，当赤道上的物体恰好能“飘”起来时，求地球自转周期T'．
如图所示，在高出水平地面h=1.8m的光滑平台上放置一质量M=2kg、由两种不同材料连接成一体的薄板A，其右段长度l1=0.2m且表面光滑，左段表面粗糙．在A最右端放有可视为质点的物块B，其质量m=1kg．B与A左段间动摩擦因数μ=0.4．开始时二者均静止，现对A施加F=20N水平向右的恒力，待B脱离A（A尚未露出平台）后，将A取走．B离开平台后的落地点与平台右边缘的水平距离x=1.2m．（取g=10m/s2）求
（1）B离开平台时的速度vB．
（2）B从开始运动到刚脱离A时，B运动的时间tB和位移xB．
（3）A左端的长度l2．
粤公网安备 44130202000953号