(15分)如图所示,相距L=0.4m、电阻不计的两平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连,导轨处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直于导轨平面。质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直。t=0时起棒在水平外力F作用下以初速度v0=2m/s、加速度a=1m/s2沿导轨向右匀加速运动。求: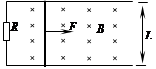
⑴t=1s时回路中的电流;
⑵t=1s时外力F大小;
⑶第1s内通过棒的电荷量。
(15分)如图所示,相距L=0.4m、电阻不计的两平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连,导轨处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直于导轨平面。质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直。t=0时起棒在水平外力F作用下以初速度v0=2m/s、加速度a=1m/s2沿导轨向右匀加速运动。求: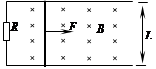
⑴t=1s时回路中的电流;
⑵t=1s时外力F大小;
⑶第1s内通过棒的电荷量。