(文)已知半径为5的圆的圆心在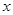 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线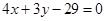 相切.
相切.
(1)求圆的标准方程;
(2)设直线
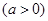 与圆相交于
与圆相交于 两点,求实数
两点,求实数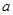 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数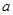 ,使得弦
,使得弦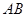 的垂直平分线
的垂直平分线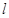 过点
过点 ,
,
相关知识点
推荐套卷
(文)已知半径为5的圆的圆心在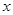 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线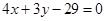 相切.
相切.
(1)求圆的标准方程;
(2)设直线
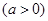 与圆相交于
与圆相交于 两点,求实数
两点,求实数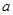 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数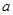 ,使得弦
,使得弦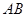 的垂直平分线
的垂直平分线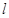 过点
过点 ,
,