一个平板小车置于光滑水平面上，其右端恰好和一个1/4光滑圆弧轨道AB的底端等高对接，如图所示。已知小车质量M=2kg，小车足够长，圆弧轨道半径R=0.8m。现将一质量m=0.5kg的小滑块，由轨道顶端A点无初速释放，滑块滑到B端后冲上小车。滑块与小车上表面间的动摩擦因数μ=0.2，g取10m/s2。求：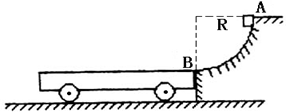
（1）滑块到达B端时，速度为多少？对轨道的压力多大？
（2）经多长的时间物块与小车相对静止？
（3）小车运动2s时，小车右端距轨道B端的距离。
(18分)如图所示，劲度系数k＝100N/m的一根轻质弹簧，右端固定在竖直墙壁上，左端连接一质量m＝1.0kg的小物块，开始时弹簧处于原长，小物块静止于O点，现将小物块缓慢向左拉动至A点后释放，让小物块沿水平面向右运动起来，已知OA长度L＝0.25m，小物块与水平面间的动摩擦因数μ＝0.1，最大静摩擦力可看成等于滑动摩擦力的大小，g取10m/s2。
⑴试在坐标纸中作出小物块在由O移动到A的过程中，弹簧弹力F随伸长量x变化的F-x图象，类比于由v-t图象求位移的方法，求此过程中克服弹簧弹力做的功W；
⑵求小物块从A点向右运动过程中的最大速度v；
⑶求小物块从A点开始运动后，第一次到达最右端时，弹簧的形变量；
⑷求小物块从A点开始运动直至静止的总路程。
(16分)如图所示，让一可视为质点的小球从光滑曲面轨道上的A点无初速滑下，运动到轨道最低点B后，进入半径为R的光滑竖直圆轨道，并恰好通过轨道最高点C，离开圆轨道后继续在光滑平直轨道上运动到D点后抛出，最终撞击到搁在轨道末端点和水平地面之间的木板上，已知轨道末端点距离水平地面的高度为H＝0.8m，木板与水平面间的夹角为θ＝37°，小球质量为m＝0.1kg，A点距离轨道末端竖直高度为h＝0.2m，不计空气阻力。(取g＝10m/s2，sin37°＝0.6，cos37°＝0.8)
⑴求圆轨道半径R的大小；
⑵求小球从轨道末端点冲出后，第一次撞击木板时的位置距离木板上端的竖直高度有多大；
⑶若改变木板的长度，并使木板两端始终与平台和水平面相接，试通过计算推导小球第一次撞击木板时的动能随木板倾角θ变化的关系式，并在图中作出Ek-(tanθ)2图象。
(14分)如图所示，质量为m＝2kg的小球穿在长L＝1m的轻杆顶部，轻杆与水平方向成θ＝37°的夹角，将小球由静止释放，1s后小球恰好到达轻杆底端，取g＝10m/s2，sin37°＝0.6，cos37°＝0.8，求：
⑴小球到达杆底时重力对它做功的功率；
⑵小球与轻杆之间的动摩擦因数μ；
⑶若在竖直平面内对小球施加一个垂直于轻杆方向的恒力F，小球从静止释放后，将以大小为1m/s2的加速度向下运动，则恒力F大小为多大？
(12分)如图所示，一长为L的长方形木块在水平地面上由静止开始以加速度a做匀加速直线运动，先后经过A、B两点位置，且通过A、B两点所用的时间分别为t1和t2，求：
⑴木块分别通过位置A、B的平均速度大小；
⑵木块前端P点到达位置A时的瞬时速度；
⑶木块前端P在A、B之间运动所需的时间。
粤公网安备 44130202000953号