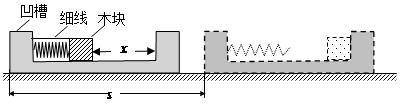
如图，水平地面上，质量为4m的凹槽被一特殊装置锁定处于静止状态，凹槽内质量为m的小木块压缩轻质弹簧后用细线固定（弹簧与小木块不粘连），此时小木块距离凹槽右侧为x；现细线被烧断，木块被弹簧弹出后与凹槽碰撞并粘连，同时装置锁定解除；此后木块与凹槽一起向右运动，测得凹槽在地面上移动的距离为s；设凹槽与地面的动摩擦因数为μ1，凹槽内表面与木块的动摩擦因数为µ2，重力加速度为g，求：
（1）木块与凹槽碰撞后瞬间的共同速度大小v；
（2）细线被烧断前弹簧储存的弹性势能。
如图所示，质量为m的小球自由下落d后，沿竖直面内的固定轨道ABC运动，AB是半径为d的四分之一粗糙圆弧，BC是直径为d的光滑半圆弧，B是轨道的最低点，小球运动到C点对轨道的压力恰为零。求小球在AB圆弧上运动过程中，克服摩擦力做了多少功？
一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小。已知地球半径R=6400km，地球表面重力加速度g=10m/s2.
如图所示，飞行员的质量为m=60kg，重力加速度为g=10m/s2，他驾驶飞机在竖直平面内做翻筋斗的圆周运动，当飞机飞到最高点时速度为
，飞行员对机座的压力恰好为零，则轨道半径R=m，若飞机飞到最低点时速度为
，飞行员对机座的压力N=N。
某恒星远处有一颗行星，靠近行星周围有众多的卫星，且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动，通过天文观测，测得离该行星最近的一颗卫星运动的轨道半径为
，周期为
。已知万有引力常量为G。
（1）求该行星的质量；
（2）通过天文观测，发现离该行星很远处还有一颗卫星，其运动的轨道半径为
，周期为
，试估算该行星周围众多卫星的总质量。
（3）通过天文观测发现，某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上，求再经过多长时间它们又将分布在一条直线上。
的初速度沿斜面上滑，同时在物体A的正上方，物体B以某一初速度
水平抛出。如果当A上滑到最高点时恰好被B物体击中（A、B均可看作质点， sin37°=0.6，cos37°=0.8，g取10m/s2）。求：
粤公网安备 44130202000953号