如图所示,空间有相互垂直的匀强电场和匀强磁场交界于虚线,电场强度为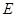 ,虚线下方匀强磁场范围足够大,磁感应强度为
,虚线下方匀强磁场范围足够大,磁感应强度为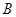 ,现有质量为
,现有质量为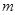 、电量为
、电量为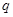 的带正电粒子从距电磁场边界
的带正电粒子从距电磁场边界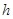 处无初速释放(带电粒子重力可忽略不计).求:
处无初速释放(带电粒子重力可忽略不计).求: 
(1)带电粒子刚离开电场时速度大小;
(2)带电粒子在匀强磁场中运动的轨迹半径;
(3)带电粒子第一次在匀强磁场中运动的时间.
相关知识点
如图所示,空间有相互垂直的匀强电场和匀强磁场交界于虚线,电场强度为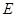 ,虚线下方匀强磁场范围足够大,磁感应强度为
,虚线下方匀强磁场范围足够大,磁感应强度为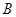 ,现有质量为
,现有质量为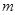 、电量为
、电量为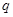 的带正电粒子从距电磁场边界
的带正电粒子从距电磁场边界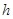 处无初速释放(带电粒子重力可忽略不计).求:
处无初速释放(带电粒子重力可忽略不计).求: 
(1)带电粒子刚离开电场时速度大小;
(2)带电粒子在匀强磁场中运动的轨迹半径;
(3)带电粒子第一次在匀强磁场中运动的时间.