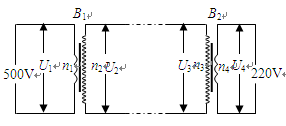
电偏转和磁偏转技术在科学上有着广泛的应用,如图所示的装置中,AB、CD间的区域有竖直方向的匀强电场,在CD的右侧有一与CD相切于M点的圆形有界匀强磁场,磁场方向垂直于纸面。一带电粒子自O点以水平初速度 正对P点进入该电场后,从M点飞离CD边界时速度为
正对P点进入该电场后,从M点飞离CD边界时速度为 ,再经磁场偏转后又从N点垂直于CD边界回到电场区域,并恰能返回O点。已知OP间距离为
,再经磁场偏转后又从N点垂直于CD边界回到电场区域,并恰能返回O点。已知OP间距离为 ,粒子质量为
,粒子质量为 ,电量为
,电量为 ,粒子自身重力忽略不计。试求:
,粒子自身重力忽略不计。试求:
(1)P、M两点间的距离;
(2)返回O点时的速度大小;
(3)磁感强度的大小和有界匀强磁场区域的面积。
相关知识点

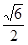 ,单色光在真空中的光速为c,求此单色光通过三棱镜的时间。
,单色光在真空中的光速为c,求此单色光通过三棱镜的时间。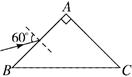
 粤公网安备 44130202000953号
粤公网安备 44130202000953号