如图1所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,已知滑块与斜面间的动摩擦因数 和滑块到斜面顶端的距离
和滑块到斜面顶端的距离 的关系如图2所示。斜面倾角为37°,长为L。有一半径
的关系如图2所示。斜面倾角为37°,长为L。有一半径 的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知:
的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知: ,
, )。求:
)。求:
(1)滑块滑至斜面底端B时的速度大小;
(2)在B点小球与滑块碰撞后小球的速度大小;
(3)滑块滑至光滑竖直半圆轨道的最高点C时对轨道的压力。

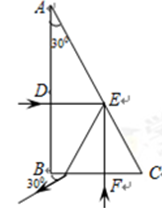

 =30°时,求粒子从射入磁场到最终离开磁场的时间t.
=30°时,求粒子从射入磁场到最终离开磁场的时间t.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号