如图所示，长木板固定在水平实验台上，在水平实验台右端地面上竖直放有一光滑的被截去八分之三(即圆心角为135°)的圆轨道；放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动，运动到长木板边缘B处撤去水平恒力F，小球水平抛出后恰好落在圆轨道C处，速度方向沿C处的切线方向，且刚好能到达圆轨道的最高点D处．已知小球的质量为m，小球与水平长木板间的动摩擦因数为μ，长木板AB长为L， B、C两点间的竖直高度为h，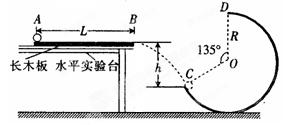
求：(1)B、C两点间的水平距离x
(2)水平恒力F的大小
(3)圆轨道的半径R
相关试题
在水平气垫导轨上有两个静止的滑块A、B，给A一个初速度
，使A与B发生正碰，碰撞后A的速度为0.5，B的速度为1.5，且方向都与A初速度方向相同。求A和B质量之间的关系。
。试确定光源离水面的距离。
如图所示，质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上，质量为2m的小孩站在小车上用力向右迅速推出木箱，木箱相对于冰面运动的速度为v，木箱运动到右侧墙壁时与竖直的墙壁发生弹性碰撞，反弹后被小孩接住，求整个过程中小孩对木箱做的功．
．在棱镜侧面
左方有一单色光源S，从S发出的光线SD以60°入射角从AB侧面中点射入三棱镜，当它从侧面AC射出时，出射光线与棱镜侧面AC间的夹角为30°．求此三棱镜的折射率并作出光路图．
粤公网安备 44130202000953号