如图,带电小球A、B(可看作点电荷)均用绝缘丝线悬挂点O点。静止时A、B相距为d,小球B的质量为m1,带电荷量为q1。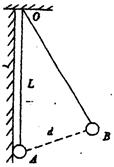
(1)若将B球带电量减到q2,平衡时AB间距离为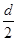 ,求q1/q2;
,求q1/q2;
(2)若将B球质量减到m2,平衡时AB间距离为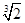 d,求m1/m2.
d,求m1/m2.
如图,带电小球A、B(可看作点电荷)均用绝缘丝线悬挂点O点。静止时A、B相距为d,小球B的质量为m1,带电荷量为q1。
(1)若将B球带电量减到q2,平衡时AB间距离为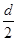 ,求q1/q2;
,求q1/q2;
(2)若将B球质量减到m2,平衡时AB间距离为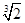 d,求m1/m2.
d,求m1/m2.