双星系统由两颗恒星组成,两恒星在相互引力的作用下分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原的k倍,两星之间的距离变为原的n倍,则此时圆周运动的周期为 ( )
A.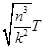 |
B.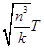 |
C. |
D.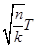 |
双星系统由两颗恒星组成,两恒星在相互引力的作用下分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原的k倍,两星之间的距离变为原的n倍,则此时圆周运动的周期为 ( )
A.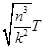 |
B.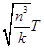 |
C. |
D.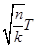 |