图l中,质量为 的物块叠放在质量为
的物块叠放在质量为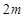 的足够长的木板上方右侧,木板放在光滑的水平地面上,物块与木板之间的动摩擦因数为
的足够长的木板上方右侧,木板放在光滑的水平地面上,物块与木板之间的动摩擦因数为 =0.2.在木板上施加一水平向右的拉力F,在0~3s内F的变化如图2所示,图中F以
=0.2.在木板上施加一水平向右的拉力F,在0~3s内F的变化如图2所示,图中F以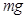 为单位,重力加速度
为单位,重力加速度 .整个系统开始时静止.
.整个系统开始时静止.
(1)求1s末木板与物块各自的速度.
(2)求2s末木板与物块各自的速度.
(3)在同一坐标系中画出0~3s内木板和物块的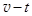 图象,据此求0~3s内物块相对于木板滑过的距离。
图象,据此求0~3s内物块相对于木板滑过的距离。
图l中,质量为 的物块叠放在质量为
的物块叠放在质量为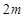 的足够长的木板上方右侧,木板放在光滑的水平地面上,物块与木板之间的动摩擦因数为
的足够长的木板上方右侧,木板放在光滑的水平地面上,物块与木板之间的动摩擦因数为 =0.2.在木板上施加一水平向右的拉力F,在0~3s内F的变化如图2所示,图中F以
=0.2.在木板上施加一水平向右的拉力F,在0~3s内F的变化如图2所示,图中F以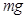 为单位,重力加速度
为单位,重力加速度 .整个系统开始时静止.
.整个系统开始时静止.
(1)求1s末木板与物块各自的速度.
(2)求2s末木板与物块各自的速度.
(3)在同一坐标系中画出0~3s内木板和物块的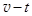 图象,据此求0~3s内物块相对于木板滑过的距离。
图象,据此求0~3s内物块相对于木板滑过的距离。