(12分)如图所示，倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接，O为轨道圆心，BC为圆轨道直径且处于竖直平面内，A、C两点等高。质量m=1kg的滑块（可视为质点）从A点由静止开始下滑，恰能滑到与O等高的D点，g取10m/s2。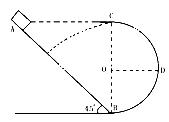
（1）求滑块与斜面间的动摩擦因数μ；
（2）若使滑块能到达C点，求滑块至少从离地多高处由静止开始下滑；
（3）若滑块离开C处后恰能垂直打在斜面上，求滑块经过C点时对轨道的压力。
在原子反应堆中抽动液态金属或在医疗器械中抽动血液等导电液体时，常使用电磁泵.某种电磁泵的结构如图所示，把装有液态钠的矩形截面导管（导管是环形的，图中只画出其中一部分）水平放置于匀强磁场中，磁场的磁感应强度为B，方向与导管垂直，让电流I按如图方向纵向穿过液态钠且电流方向与B垂直.设导管截面高为a，宽为b，导管有长为l的一部分置于磁场中，由于磁场对液态钠的作用力使液态钠获得驱动力而不断沿管子向前推进.整个系统是完全密封的，只有金属钠本身在其中流动，其余的部件是固定不动的。
（1）在图上标出液态钠受磁场驱动力的方向;
（2）假定在液态钠不流动的条件下，求导管横截面上由磁场驱动力所形成的附加压强p与上述各量的关系式;
（3）设液态钠中每个自由电荷所带电荷量为q，单位体积内参与导电的自由电荷数为n，求在横穿液态钠的电流I的方向上参与导电的自由电荷定向移动的平均速度
.
过山车是游乐场中常见的设施．如图17所示是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径R1=2.0m、R2=1.4m．一个质量为m=1.0kg的小球（视为质点），从轨道的左侧A点以v0=12.0m/s的初速度沿轨道向右运动，A、B间距L1=6.0m．小球与水平轨道间的动摩擦因数μ=0.2，圆形轨道是光滑的．假设水平轨道足够长，圆形轨道间不相互重叠．重力加速度取g=10m/s2，计算结果保留小数点后一位数字．试求：
（1）小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
（2）如果小球恰能通过第二圆形轨道，B、C间距
应是多少；
（3）在满足（2）的条件下，如果要使小球不能脱离轨道，在第三个圆形轨道的设计中，半径R3应满足的条件和小球最终停留点与起点间的距离．
如图所示，绝缘的水平桌面上方有一竖直方向的矩形区域，该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的，且矩形的下边EH与桌面相接．三个正方形区域中分别存在方向为竖直向下、竖直向上、竖直向上的匀强电场，其场强大小比例为1:1:2．现有一带正电的滑块以某一初速度从E点射入场区，初速度方向水平向右，滑块最终恰从D点射出场区．已知滑块在ABFE区域所受静电力和所受重力大小相等，桌面与滑块之间的滑动摩擦因素为0.125，重力加速度为g，滑块可以视作质点．求：
（1）滑块进入CDHG区域时的速度大小．
（2）滑块在ADHE区域运动的总时间．
如图中（a）所示，一倾角为37o的传送带以恒定速度运行．现将一质量m=2kg的小物体以某一初速度放上传送带，物体相对地面的速度随时间变化的关系如图（b）所示．（取沿传送带向上为正方向，g=10m/s2，sin37o=0.6，cos37o=0.8）求：
（1）0~10s内物体位移的大小；
（2）物体与传送带间的动摩擦因数；
（3）0~10s内物体机械能增量及与传送带摩擦产生的热量Q．
粤公网安备 44130202000953号