如图所示，在一圆形管道内封闭有理想气体，用一固定活塞K和不计质量可自由移动的活塞A，将管内气体分割成体积相等的两部分。固定活塞K、可动活塞A和管道中心O处于同一水平线上。管道内气体温度都为T0=300K，压强都为P0=1.0×105Pa。现保持管道下部分气体温度不变，只对管道上部分气体缓慢加热，当可动活塞P缓慢移动到管道最低点时（不计摩擦），求；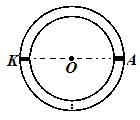
①下部分气体的压强；
②上部分气体的温度。
如图所示，飞机距地面高度为H，水平飞行速度v0，地面上停着一辆汽车，与飞机水平距离为X，欲使飞机投出炸弹击中汽车，H、v0、X应满足什么关系？(重力加速度为g)．
如图甲所示，一对足够长的平行光滑轨道放置在水平面上，两轨道相距L=1m，左端之间用R=3Ω的电阻连接，轨道的电阻忽略不计。一质量m=0.5kg、电阻r=1Ω的导体杆静置于两轨道上，并与两轨道垂直。整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直轨道平面向上。现用水平拉力沿轨道方向拉导体杆，拉力F与导体杆运动的位移x间的关系如图乙所示。当拉力达到最大时，导体杆恰好开始做匀速运动。当位移x=2.5m时撤去拉力，导体杆又滑行了一段距离△x后停下，已知在滑行△x的过程中电阻R上产生的焦耳热为12J。求：
（1）拉力F作用过程中，通过电阻R上的电量q；
（2）导体杆运动过程中的最大速度vm；
（3）拉力F作用过程中，回路中产生的焦耳热Q。
如图所示，水平线MN的上方区域存在场强大小为E的匀强电场，其方向指向右上方且与MN的夹角θ=45°，MN的下方区域存在磁感应强度为B的匀强磁场，其方向垂直纸面向外。一个重力不计、质量为m、电量为q的带负电粒子，从MN上的O点，以v0的初速度沿电场方向射入匀强电场，并记为第一次经过MN。求：
（1）粒子从O点出发到第二次经过MN经历的时间t；
（2）粒子第三次经过MN的位置与O之间的距离s；
（3）粒子第四次经过MN时速度v的大小。
某行星的半径为R1、自转周期为T1，它有一颗卫星，绕行星公转的轨道半径为R2、公转周期为T2。万有引力常量为G．求：
（l）该行星的质量M；
（2）要在此行星的赤道上发射一颗质量为m的靠近行星表面绕行的人造卫星，使其轨道平面与行星的赤道平面重合，设行星上无气体阻力，那么对人造卫星至少应做多少功？
粤公网安备 44130202000953号