如图,ABC三个木块的质量均为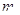 。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速
。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速 沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为
沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为 ,求弹簧释放的势能。
,求弹簧释放的势能。
如图,ABC三个木块的质量均为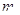 。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速
。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速 沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为
沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为 ,求弹簧释放的势能。
,求弹簧释放的势能。