如图所示,固定在竖直平面内倾角为 的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量
的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量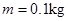 的小物块,从高为
的小物块,从高为 处静止释放,沿轨道AB滑下,并滑上倾角也为
处静止释放,沿轨道AB滑下,并滑上倾角也为 的轨道BC,所能达到的最大高度是
的轨道BC,所能达到的最大高度是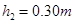 。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知
。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知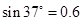 ,
,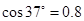 ,取g=10m/s2,求:
,取g=10m/s2,求: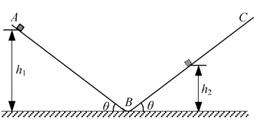
(1) 物块从释放到第一次速度为零的过程中,重力所做的功;
(2) 物块与轨道间的动摩擦因数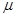 。
。
如图所示,固定在竖直平面内倾角为 的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量
的直轨道AB,与倾角可调的足够长的直轨道BC顺滑连接。现将一质量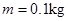 的小物块,从高为
的小物块,从高为 处静止释放,沿轨道AB滑下,并滑上倾角也为
处静止释放,沿轨道AB滑下,并滑上倾角也为 的轨道BC,所能达到的最大高度是
的轨道BC,所能达到的最大高度是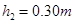 。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知
。若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失。已知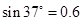 ,
,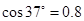 ,取g=10m/s2,求:
,取g=10m/s2,求:
(1) 物块从释放到第一次速度为零的过程中,重力所做的功;
(2) 物块与轨道间的动摩擦因数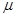 。
。