如图所示,带正电小球质量为m=1×10-2kg,带电量为q=l×10-6C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时,该小球从静止开始始终沿水平面做匀加速直线运动,当运动到B点时,测得其速度vB =1.5m/s,此时小球的位移为S=0.15m.设电场方向与水平面之间夹角为θ,讨论并求此匀强电场场强E的取值范围.(g=10m/s2。)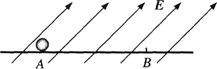
如图所示,带正电小球质量为m=1×10-2kg,带电量为q=l×10-6C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时,该小球从静止开始始终沿水平面做匀加速直线运动,当运动到B点时,测得其速度vB =1.5m/s,此时小球的位移为S=0.15m.设电场方向与水平面之间夹角为θ,讨论并求此匀强电场场强E的取值范围.(g=10m/s2。)