某同学用双缝干涉实验测量红光的波长,他将测量头的分划板的中心刻线与某亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图乙所示设为x1,然后同方向转动测量头,使分划板中心刻线与第6条亮纹的中心对齐,此时手轮上的示数如图丙所示设x2.则相邻亮纹的间距Δx的计算式为Δx= (用x1 x2表示),代入数据求得Δx= mm.若双缝间距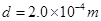 ,测得双缝到屏的距离
,测得双缝到屏的距离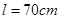 ,则求得所测红光波长为 m。
,则求得所测红光波长为 m。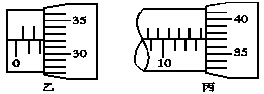
某同学用双缝干涉实验测量红光的波长,他将测量头的分划板的中心刻线与某亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图乙所示设为x1,然后同方向转动测量头,使分划板中心刻线与第6条亮纹的中心对齐,此时手轮上的示数如图丙所示设x2.则相邻亮纹的间距Δx的计算式为Δx= (用x1 x2表示),代入数据求得Δx= mm.若双缝间距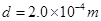 ,测得双缝到屏的距离
,测得双缝到屏的距离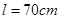 ,则求得所测红光波长为 m。
,则求得所测红光波长为 m。