质量为2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数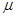 =0.40,求:
=0.40,求: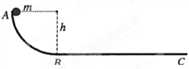
(1)物体滑至B点时速度的大小;(2)物体最后停止在离B点多远的位置上.
质量为2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数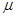 =0.40,求:
=0.40,求:
(1)物体滑至B点时速度的大小;(2)物体最后停止在离B点多远的位置上.