如图所示,在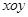 平面内有一扇形金属框
平面内有一扇形金属框 ,其半径为
,其半径为 ,
, 边与
边与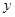 轴重合,
轴重合,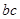 边与
边与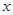 轴重合,且
轴重合,且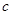 为坐标原点,
为坐标原点, 边与
边与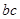 边的电阻不计,圆弧
边的电阻不计,圆弧 上单位长度的电阻为
上单位长度的电阻为 。金属杆MN长度为L,放在金属框
。金属杆MN长度为L,放在金属框 上,MN与
上,MN与 边紧邻,金属杆ac长度的电阻为R0。磁感应强度为B的匀强磁场与框架平面垂直并充满平面。现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为
边紧邻,金属杆ac长度的电阻为R0。磁感应强度为B的匀强磁场与框架平面垂直并充满平面。现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为 。求:
。求:
(1)在MN杆运动过程中,通过杆的电流I与转过的角度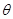 间的关系;
间的关系;
(2)整个电路消耗电功率的最小值是多少?
如图所示,在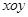 平面内有一扇形金属框
平面内有一扇形金属框 ,其半径为
,其半径为 ,
, 边与
边与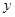 轴重合,
轴重合,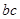 边与
边与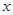 轴重合,且
轴重合,且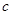 为坐标原点,
为坐标原点, 边与
边与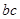 边的电阻不计,圆弧
边的电阻不计,圆弧 上单位长度的电阻为
上单位长度的电阻为 。金属杆MN长度为L,放在金属框
。金属杆MN长度为L,放在金属框 上,MN与
上,MN与 边紧邻,金属杆ac长度的电阻为R0。磁感应强度为B的匀强磁场与框架平面垂直并充满平面。现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为
边紧邻,金属杆ac长度的电阻为R0。磁感应强度为B的匀强磁场与框架平面垂直并充满平面。现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为 。求:
。求:
(1)在MN杆运动过程中,通过杆的电流I与转过的角度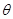 间的关系;
间的关系;
(2)整个电路消耗电功率的最小值是多少?