如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持V0=2m/s的速率顺时针运行。现把一质量m=10kg的工件(可看为质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.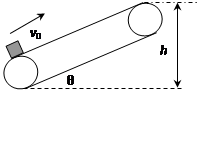
求(1)工件与皮带间的动摩擦因数。
(2)电动机由于传送工件多消耗的电能。
如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持V0=2m/s的速率顺时针运行。现把一质量m=10kg的工件(可看为质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.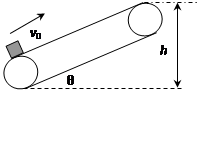
求(1)工件与皮带间的动摩擦因数。
(2)电动机由于传送工件多消耗的电能。