如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取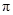 =3
=3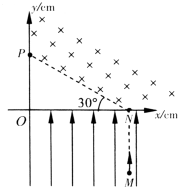
求:
(1)粒子在磁场中运动的速度v;
(2)粒子在磁场中运动的时间t;
(3)匀强电场的电场强度E.
如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取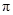 =3
=3
求:
(1)粒子在磁场中运动的速度v;
(2)粒子在磁场中运动的时间t;
(3)匀强电场的电场强度E.