将一个重物用弹簧秤竖直悬挂起来后,弹簧秤的示数如图A所示(弹簧秤的量程100N),之后将该物体放到粗糙的水平面上如图17B所示,当逐渐增大拉力到43N时,物体刚好运动,物体运动之后只用40N的拉力就能保持向右匀速运动( )。求:
)。求: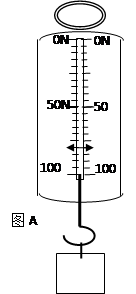

(1)物体的质量为多少千克?物体与地面的最大静摩擦力为多大?
(2)物体与地面间的动摩擦因素为多大?
(3)如果将拉力改为60N,并且由静止拉物体运动,经过时间为10秒时物体的运动速度和位移各为多少?
将一个重物用弹簧秤竖直悬挂起来后,弹簧秤的示数如图A所示(弹簧秤的量程100N),之后将该物体放到粗糙的水平面上如图17B所示,当逐渐增大拉力到43N时,物体刚好运动,物体运动之后只用40N的拉力就能保持向右匀速运动( )。求:
)。求:

(1)物体的质量为多少千克?物体与地面的最大静摩擦力为多大?
(2)物体与地面间的动摩擦因素为多大?
(3)如果将拉力改为60N,并且由静止拉物体运动,经过时间为10秒时物体的运动速度和位移各为多少?