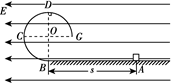
如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为 的正点电荷。O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
的正点电荷。O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb= 。一质量为m、电荷量为+q的小滑块(可视为质点)以初动能
。一质量为m、电荷量为+q的小滑块(可视为质点)以初动能 从a点出发,沿AB直线向b点运动,其中小滑块第一次经过O点时的动能为
从a点出发,沿AB直线向b点运动,其中小滑块第一次经过O点时的动能为 ,第一次到达b点时的动能恰好为零,已知静电力常量为
,第一次到达b点时的动能恰好为零,已知静电力常量为 。求:
。求:
(1)两个带电量均为 的正点电荷在a点处的合场强大小和方向;
的正点电荷在a点处的合场强大小和方向;
(2)小滑块由a点向b点运动的过程中受到的滑动摩擦力大小;
(3)aO两点间的电势差。
相关知识点

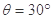 .一个质量
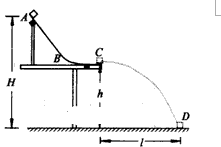
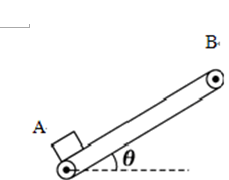
.一个质量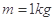 的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数
的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数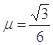 ,取
,取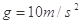 .试求:
.试求: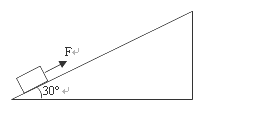
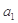 ;
;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号