如图所示，水平放置的平行板电容器，原来AB两板不带电，B极板接地，它的极板长L= 0．1m，两板间距离d = 0．4 cm，现有一微粒质量m=2．0×10-6kg，带电量q=+1．0×10-8C，以一定初速度从两板中央平行于极板射入，由于重力作用微粒恰好能落到A板上中点O处，取g=10m/s2．试求：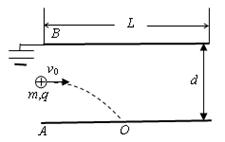
（1）带电粒子入射初速度的大小；
（2）现使电容器带上电荷，使带电微粒能从平行板电容器的右侧射出，则带电后A板的电势为多少？
如图a所示，气缸内利用活塞封闭有一定量的理想气体，平时储存在
的冰水混合物中，体积为
，取出后置于
的室内，稳定后如图b所示。不计一切摩擦阻力，大气压不变。
①气缸内气体在室内的体积；
②气缸内气体从冰水混合物到室内的过程是从外界吸热还是向外界放热？
半径为
的圆形区域内存在垂直平面向外的匀强磁场，平行金属板M和N的中线O1O2与圆形O在同一水平线上，两金属板间距为，长为
，电压为
。一个质量为
带电荷量为
的粒子以速度
从圆周的P点沿半径方向垂直金属板中心线O1O2进入匀强磁场区域，后沿中心线O1O2进入金属板间匀强电场，从右端飞出，不计粒子重力，则
（1）磁场的磁感应强度B的大小；
（2）粒子在磁场和电场中运动的总时间；
（3）当粒子在电场中经过时间
时，突然改变两金属板带电性质，使电场反向，且两板间电压变为U1，则粒子恰好能从O2点飞出电场，求电压U1和U0的比值.
的带电荷量
的小球从某一点静止释放，运动
秒后空间出现竖直方向的匀强电场，再经过如图1所示，固定于绝缘水平面上且间距d = 0.2m的U型金属框架处在竖直向下、均匀分布的磁场中，磁场的左边界cd与右边界ab之间的距离L = 1m。t=0时，长为d的金属棒MN从ab处开始沿框架以初速度υ0 = 0.2m/s向左运动，t = 5s时棒刚好达到cd处停下；t＝0时刻开始，磁场的磁感应强度B的倒数随时间t的变化规律如图2所示。电阻R = 0.4Ω，棒的电阻r = 0.1Ω，不计其他电阻和一切摩擦阻力，棒与导轨始终垂直且接触良好。求：
（1）在0~1s内棒受到的安培力；
（2）棒的质量m；
（3）在0~5s内电阻R消耗的平均电功率P1。
粤公网安备 44130202000953号