如图所示，电阻R1 = 2Ω，小灯泡L上标有“3V，1.5W”（灯泡的电阻不随温度变化），电源内阻r = 1Ω，滑动变阻器的最大阻值为R0（大小未知）.当触头P滑动到最上端 a时, 安培表的读数为l A（其电阻不计），小灯泡L恰好正常发光，求：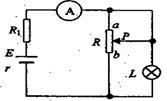
(1)滑动变阻器的最大阻值R0；
(2)电源的电动势E多大;
(3)当触头P滑动到最下端 b时电源的效率多大?
如图所示，有一带负电的小球，其带电量
=-2×10-3
．开始时静止在场强
=200
的匀强电场中的
点，靠近电场极板
有一挡板
，小球与挡板的距离
=5cm，与
板距离
=45cm，重力作用不计．在电场力作用下小球向左运动，与挡板相碰后电量减少到碰前的
倍，已知
，假设碰撞过程中小球的机械能没有损失。
(1)设匀强电场中挡板所在位置处电势为零，则电场中点的电势为多少?并求出小球第一次到达挡板时的动能；
(2)求出小球第一次与挡板相碰后向右运动的距离；
(3)小球经过多少次碰撞后，才能抵达板?(取
g1.2="0.08) "
质量为
=1
的小物块轻轻放在水平匀速运动的传送带上的
点，随传送带运动到
点后水平抛出，小物块恰好无碰撞的沿圆弧切线从
点进入竖直光滑圆孤轨道下滑。、
为圆弧的两端点，其连线水平，斜面与圆弧轨道在点相切连接(小物块经过点时机械能损失不计)。已知圆弧半径
=1.0，圆弧对应圆心角
=1060，轨道最低点为
，点距水平面的高度
=0.8。设小物块首次经过点时为零时刻，在
=0.8s时刻小物块经过
点，小物块与斜面间的滑动摩擦因数为
。空气阻力不计(g=10
，sin370=0.6，cos370=0.8)试求：
(1)小物块离开点的水平初速度％大小；
(2)小物块经过点时对轨道的压力； ．
(3)斜面上
间的距离。
如图所示，水平放置的平行板电容器，原来两板不带电，上极板接地，它的极板长
=0.1
，两板间距离
=0.4
，有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入，由于重力作用微粒能落到下板上，已知微粒质量=2.0×10-6
，电量
=1.0×10-8
，电容器电容=1.0×10-6
，取g=lO
．试求：
(1)若第一个粒子刚好落到下板中点
处，则带电粒子入射初速度的大小；
(2)两板间电场强度为多大时，带电粒子能刚好落下板右边缘
点；
(3)落到下极板上带电粒子总的个数．
列车在机车的牵引下沿平直铁轨匀加速行驶，在
=100
内速度由
=5.0
增加到
=15．O。
(1)求列车的加速度大小；
(2)若列车的质量是
=1．0×106
，机车对列车的牵引力是
=1．5×105
，求列车在运动中所受的阻力大小；
(3)求此过程中机车牵引力做的功．
粤公网安备 44130202000953号