如图是某种静电分选器的原理示意图．两个竖直放置的平行金属板带有等量异号电荷，形成匀强电场．分选器漏斗的出口与两板上端处于同一高度，到两板距离相等．混合在一起的a、b两种颗粒从漏斗出口下落时，a种颗粒带上正电，b种颗粒带上负电．经分选电场后，a、b两种颗粒分别落到水平传送带A、B上．
已知两板间距d=0．1 m，板的长度l=0．5m，电场仅局限在平行板之间；各颗粒所带电量大小与其质量之比均为1 x10-5G/kg．设颗粒进入电场时的初速度为零，分选过程中颗粒大小及颗粒间的相互作用力不计．要求两种颗粒离开电场区域时，不接触到极板但有最大偏转量，重力加速度g取10m/s2．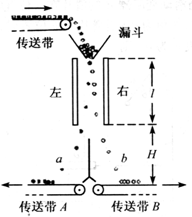
（1）左右两板各带何种电荷?两极板间的电压多大?
（2）若两带电平行板的下端距传送带4、B的高度H=0．3m，颗粒落至传送带时的速度大小是多少?
（3）设颗粒每次与传送带碰撞反弹时，沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半．写出颗粒第n次碰撞反弹高度的表达式．并求出经过多少次碰撞，颗粒反弹的高度小于0．01m．
我国第一艘航母“辽宁号”于2011年11月29日进行了第二次海试。据媒体报道，此次海试进行了舰载机测试，“拦阻索”是在飞机降落在甲板上时挂住飞机尾钩、增加向后的阻力减少滑行距离的装置。若一架质量为m=3×104kg的舰载机以v0=80m/s的速度降落在航母甲板上，滑行s=160m恰好停下，求：
（1）飞机滑行时的加速度a；
（2）飞机滑行的时间t；
（3）飞机滑行过程受到的平均阻力f。
一同学在a=2m/s2匀加速下降的升降机中最多能举起m1=75kg的物体。取g=10m/s2，求：
（1）此人在地面上可举起物体的最大质量；
（2）若该同学在一匀加速上升的升降机中最多能举起m2=50kg的物体，则该升降机上升的加速度为多大？
如图（甲）所示，两足够长的平行光滑的金属导轨MN，PQ相距为L=1m，导轨平面与水平面夹角α=37°，导轨电阻不计.磁感应强度为B1=2T的匀强磁场垂直于导轨平面向上，长为L=1m的金属杆ab垂直于MN，PQ放置在导轨上，且始终与导轨接触良好，金属杆的质量为m1=2kg、电阻为R1=3Ω.两金属导轨的上端连接右侧电路，电路中通过导线接一对水平放置的平行金属板，两板间距离和板长均为d=1m，定值电阻为R2=1Ω.现闭合开关S并将金属杆由静止释放，取重力加速度g=10m/s2.
（1）求金属杆沿导轨下滑的最大速率vm；
（2）当金属杆稳定下滑时，在水平放置的平行金属板间加一垂直于纸面向里的匀强磁场B2=3T，在下板的右端C点且非常靠近下板的位置有一质量为m2=6×10-5kg、带电量为q=-1×10-4C的液滴以初速度v水平向左射入磁场，该液滴可视为质点，要使带电液滴能从金属板间射出，则初速度v满足什么条件？
（3）若带电液滴射入的速度恰好使液滴从D点飞出，液滴从C点射入时，再从该磁场区域加一个如图（乙）所示的变化磁场（正方向与B2方向相同，不考虑磁场变化所产生的电场），求该带电液滴从C点射入到运动到D点所经历的时间t.
一绝缘“U”型杆由两段相互平行的足够长的竖直直杆PQ、MN和一半径为R的光滑半圆环QAN组成.固定在竖直平面内，其中杆PQ是光滑的，杆MN是粗糙的，整个装置处在水平向右的匀强电池中.在QN连线下方区域足够大的范围内同时存在垂直竖直平面向外的匀强磁场，磁感应强度为
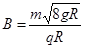.现将一质量为m、带电量为-q（q＞0）的小环套在PQ杆上，小环所受的电场力大小为其重力的3倍.（重力加速度为g）.求：
（1）若将小环由C点静止释放，刚好能达到N点，求CQ间的距离；
（2）在满足（1）问的条件下，小环第一次通过最低点A时受到圆环的支持力的大小；
（3）若将小环由距Q点8R处静止释放，设小环与MN杆间的动摩擦因数为u，小环所受最大静摩擦力大小相等，求小环在整个运动过程则克服摩擦力所做的功.
粤公网安备 44130202000953号