如图所示，在光滑绝缘水平桌面上有两个静止的小球A和B，B在桌边缘，A和B均可视为质点，质量均为m=0．2kg，A球带正电，电荷量q=0．1C，B球是绝缘体不带电，桌面距地面的高h=0.05m．开始时A、B相距L=0．1m，在方向水平向右、大小E=10N／C的匀强电场的电场力作用下，A开始向右运动，并与B球发生正碰，碰撞中A、B的总动能无损失，A和B之间无电荷转移．求：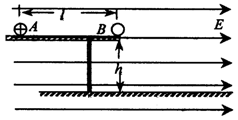 
(1)A经过多长时间与B碰撞?
(2)A、B落地点之间的距离是多大?
如图所示，在一个矩形区域abcd内，有两个方向相反且都垂直纸面的匀强磁场分布在以对角线bd为边界的两个区域Ⅰ、Ⅱ内，已知ab边长为
，ad与ac夹角为
＝300。一质量为
带电量为
的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场，随后粒子经过ac与bd交点o进入Ⅱ区（粒子重力不计）。
求Ⅰ区的磁感应强度
的方向和大小如果粒子最终能从cd边射出磁场，求Ⅱ区磁感应强度
应满足的条件
如图所示，两根金属导轨平行放置在倾角为
30°的斜面上，导轨左端接有电阻，
导轨自身电阻不计．匀强磁场垂直于斜面向上，磁感应强度为
．质量为 
，电阻为
的金属棒ab由静止释放，沿导轨下滑，如图所示．设导轨足够长，导轨宽度
，金属棒ab下滑过程中始终与导轨接触良好，当金属棒下滑的高度为
时，恰好达到最大速度vm=2m/s，求此过程中：
金属棒受到的摩擦阻力；
电阻R中产生的热量；
通过电阻R的电量．
如图所示，为某一装置的俯视图，PQ、MN为竖直放置的很长的平行金属薄板，两板间有匀强磁场，它的磁感应强度大小为B，方向竖直向下，金属棒AB搁置在两板上缘，并与两板垂直，现有质量为m、带电量大小为q，其重力不计的粒子，以初速度v0水平射入两板问．问：
金属棒AB应朝什么方向、以多大的速度运动，可以使带电粒
子做匀速运动?若金属棒运动停止，带电粒子在磁场中继续运动时，位移第一次到达
时的时间间隔是多少？
温度传感器广泛应用于室内空调、电冰箱和微波炉等家用电器产品中，它是利用热敏电阻的阻值随温度而变化的特性工作的。在右图中已知电源的电动势为
，内电阻可以忽略不计；G为灵敏电流表，内阻
保持不变，R为热敏电阻，其电阻值与温度的变化关系如右图中
图线所示。闭合开关，当R的温度等于20℃时，电流表示数
mA，当电流表的示数
=3.6mA时，热敏电阻R的温度是多少℃？
如图所示，位于竖直平面内的坐标系xoy，在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场，磁感应强度大小为B=0.5T，还有沿x轴负方向的匀强电场，场强大小为E=2N/C．在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场，并在y>h=0.4m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场．一个带电荷量为q的油滴从图中第三象限的P点得到一初速度，恰好能沿PO作匀速直线运动（PO与x轴负方向的夹角为θ=45O），并从原点O进入第一象限．已知重力加速度g=10m/s2，问：
油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比，并指出油滴带何种电荷；
油滴在P点得到的初速度大小?
油滴在第一象限运动的时间。
粤公网安备 44130202000953号