如图所示，轻杆的一端有一个小球，另一端有光滑的固定轴O．现给球一初速度，使球和杆一起绕O轴在竖直面内转动，不计空气阻力，用F表示球到达最高点时杆对小球的作用力，则F ( )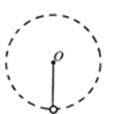
| A．一定是拉力 | B．一定是推力 |
| C．一定定于0 | D．可能是拉力，可能是推力，可能等于0 |
相关试题
如图所示，a、b两斜线分别表示从同一地点沿同一方向的两物体做直线运动时的速度图象，下列说法正确的是 （）
| A．前10s内b的位移比较大 |
| B．10s时a、b两物体相遇 |
| C．10s末a、b两物体速度相等 |
| D．a的加速度比b的加速度大 |
竖直升空的火箭，其速度图象如图所示，由图可知（）
| A．火箭上升到最高点所用时间是40s |
| B．火箭前40s上升，以后下降 |
| C．火箭的加速度始终是20m/s2 |
| D．火箭离地最大的高度是48000m |
小球从离地板5m高处落下，又被地板弹回，在离地板2m高处被接住．则小球通过的路程和位移大小分别是( )
| A．7 m， 7m | B．5m，2m | C．5m，3m | D．7m，3m |
下列说法中正确的是( )
| A．物体运动的速度越大，加速度也一定越大 |
| B．物体的加速度越大，它的速度一定越大 |
| C．加速度就是“增加出来的速度” |
| D．加速度反映速度变化的快慢，与速度、速度的变化量无关 |
粤公网安备 44130202000953号