如图所示，竖直平面内有足够长的金属导轨，轨距0.2m，金属导体ab可在导轨上无摩擦地上下滑动，ab的电阻为0.4Ω，导轨电阻不计，导轨ab的质量为0.2g，垂直纸面向里的匀强磁场的磁应强度为0.2T，且磁场区域足够大，当ab导体自由下落0.4s时，突然接通电键K，则：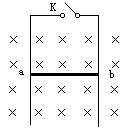
（1）试说出K接通后，ab导体的运动情况。
（2）ab导体匀速下落的速度是多少？（g取10m/s2）
我国的“探月工程”计划将于2017年宇航员登上月球。若宇航员登上月球后，在距离月球水平表面h高度处，以初速度v0水平拋出一个小球，测得小球从抛出点到落月点的水平距离s。求：
（1）月球表面重力加速度
的大小；
（2）小球落月时速度v的大小。
如图，竖直平面内放着两根间距L = 1m、电阻不计的足够长平行金属板M、N，两板间接一阻值R= 2Ω的电阻，N板上有一小孔Q，在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0= 1T的有界匀强磁场，N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场，磁感应强度大小分别为B1=3T和B2=2T。有一质量M = 0.2kg、电阻r =1Ω的金属棒搭在MN之间并与MN良好接触，用输出功率恒定的电动机拉着金属棒竖直向上运动，当金属棒达最大速度时，在与Q等高并靠近M板的P点静止释放一个比荷
的正离子，经电场加速后，以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力，忽略电流产生的磁场，取g=
。求：
（1）金属棒达最大速度时，电阻R两端电压U；
（2）电动机的输出功率P；
（3）离子从Q点进入右侧磁场后恰好不会回到N板，Q点距分界线高h等于多少。
如图所示，有一光滑、不计电阻且较长的“
"平行金属导轨，间距L="l" m，导轨所在的平面与水平面的倾角为3 7°，导轨空间内存在垂直导轨平面的匀强磁场。现将一质量m=0.1kg、电阻R=2
的金属杆水平靠在导轨处，与导轨接触良好。(g=l0m／s2，sin37°=0.6 cos37°=0.8)
(1)若磁感应强度随时间变化满足B=2+0.2t(T)，金属杆由距导轨顶部l m处释放，求至少经过多长时间释放，会获得沿斜面向上的加速度；
(2)若匀强磁场大小为定值，对金属杆施加一个平行于导轨斜面向下的外力F，其大小为
为金属杆运动的速度，使金属杆以恒定的加速度a=10m／s2沿导轨向下做匀加速运动，求匀强磁场磁感应强度B的大小；
(3)若磁感应强度随时间变化满足
时刻金属杆从离导轨顶端So="l" m处静止释放，同时对金属杆施加一个外力，使金属杆沿导轨下滑且没有感应电流产生，求金属杆下滑5 m所用的时间。
如图所示，电压为U的两块平行金属板MN，M板带正电。X轴与金属板垂直，原点O与N金属板上的小孔重合，在O≤X≤d区域存在垂直纸面的匀强磁场
(图上未画出)和沿y轴负方向火小为
的匀强电场，与E在y轴方向的区域足够大。有一个质量为m，带电量为q的带正电粒子(粒子重力不计)，从靠近M板内侧的P点(P点在X轴上)由静止释放后从N板的小孔穿出后沿X轴做直线运动；若撤去磁场，在第四象限X>d的某区域加上左边界与y轴平行且垂直纸面的匀强磁场B2(图上未画出)，为了使粒子能垂直穿过X轴上的Q点，Q点坐标为（
）。求
(1)磁感应强度的大小与方向；
(2)磁感应强度B2的大小与方向；
(3)粒子从坐标原点O运动到Q点所用的时间t。
如图所示，光滑的水平面AB与半径R=0.4m的光滑竖直半圆轨道BCD在B点相切，D点为半圆轨道最高点，A点的右侧连接一粗糙的水平面。用细线连接甲、乙两物体，中问夹一轻质压缩弹簧，弹簧与甲、乙两物体不拴接，甲的质量朋
=4kg，乙的质量
=5kg，甲、乙均静止。若固定乙，烧断细线，甲离开弹簧后经过B点进入半圆轨道，过D点时对轨道的压力恰好为零。取g=10m/s2，甲、乙两物体均可看作质点，求：
(1)甲离开弹簧后经过B点时的速度的大小
；
(2)在弹簧压缩量相同的情况下，若固定甲，烧断细线，乙物体离开弹簧后从A点进入动摩擦因数
=0.4的粗糙水平面，则乙物体在粗糙水平面运动的位移S。
粤公网安备 44130202000953号