一卡车拖挂一相同质量的车厢,在水平直道上以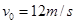 的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为
的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为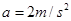 的加速度减速滑行。在车厢脱落
的加速度减速滑行。在车厢脱落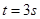 后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
一卡车拖挂一相同质量的车厢,在水平直道上以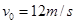 的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为
的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为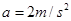 的加速度减速滑行。在车厢脱落
的加速度减速滑行。在车厢脱落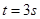 后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。