如图所示,倾角θ=30°,宽度L=1m的足够长的U形平行光滑金属导轨,固定在磁感强度B=1T,范围充分大的匀强磁场中,磁场方向与导轨平面垂直.用平行于导轨,功率恒为6W的牵引力F牵引一根质量m=0.2kg,电阻R=1Ω放在导轨上的金属棒ab,由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直),当ab棒移动2.8m时获得稳定速度,在此过程中,金属棒产生的热量为5.8J(不计导轨电阻及一切摩擦,取g=10m/s2),求:
(1)ab棒的稳定速度;
(2)ab棒从静止开始达到稳定速度所需时间.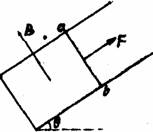
如图所示,倾角θ=30°,宽度L=1m的足够长的U形平行光滑金属导轨,固定在磁感强度B=1T,范围充分大的匀强磁场中,磁场方向与导轨平面垂直.用平行于导轨,功率恒为6W的牵引力F牵引一根质量m=0.2kg,电阻R=1Ω放在导轨上的金属棒ab,由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直),当ab棒移动2.8m时获得稳定速度,在此过程中,金属棒产生的热量为5.8J(不计导轨电阻及一切摩擦,取g=10m/s2),求:
(1)ab棒的稳定速度;
(2)ab棒从静止开始达到稳定速度所需时间.