如图所示,阴极K发射电子,阳极P和阴极K间加上电压后电子被加速。A,B是偏向板,使飞进的电子偏离。若已知P,K间所加电压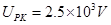 ,A,B两极板长
,A,B两极板长 ,A,B两板间距
,A,B两板间距 ,所加电压
,所加电压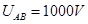 ,
,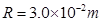 ,电子质量
,电子质量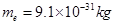 ,电子的电荷量
,电子的电荷量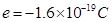 ,设从阴极出来的电子速度为零,不计重力。
,设从阴极出来的电子速度为零,不计重力。
(1)电子通过阳极P时的速度 是多大?
是多大?
(2)电子通过偏转电极时具有动能 是多大?
是多大?
(3)电子过偏转电极后到达距离偏转电极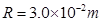 荧光屏上
荧光屏上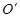 点,此点偏离入射方向的距离y是多大?
点,此点偏离入射方向的距离y是多大?
如图所示,阴极K发射电子,阳极P和阴极K间加上电压后电子被加速。A,B是偏向板,使飞进的电子偏离。若已知P,K间所加电压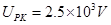 ,A,B两极板长
,A,B两极板长 ,A,B两板间距
,A,B两板间距 ,所加电压
,所加电压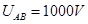 ,
,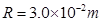 ,电子质量
,电子质量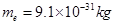 ,电子的电荷量
,电子的电荷量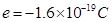 ,设从阴极出来的电子速度为零,不计重力。
,设从阴极出来的电子速度为零,不计重力。
(1)电子通过阳极P时的速度 是多大?
是多大?
(2)电子通过偏转电极时具有动能 是多大?
是多大?
(3)电子过偏转电极后到达距离偏转电极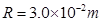 荧光屏上
荧光屏上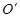 点,此点偏离入射方向的距离y是多大?
点,此点偏离入射方向的距离y是多大?