(12分)如图所示,斜面倾角为θ,木板A的质量为M,物块B的质量为m.绳的一端与B连接,另一端与固定在斜面上的挡板相连,绳与斜面平行.已知A与B间 的动摩擦因数为μ1,A与斜面间的动摩擦因数为μ2.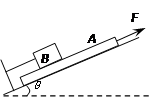
(1)若在沿斜面向上的力F作用下A正沿斜面向上匀速运动,求F的值.
(2)若将(1)中的力换成2F,求此时连接B的轻绳上的拉力大小.
(12分)如图所示,斜面倾角为θ,木板A的质量为M,物块B的质量为m.绳的一端与B连接,另一端与固定在斜面上的挡板相连,绳与斜面平行.已知A与B间 的动摩擦因数为μ1,A与斜面间的动摩擦因数为μ2.
(1)若在沿斜面向上的力F作用下A正沿斜面向上匀速运动,求F的值.
(2)若将(1)中的力换成2F,求此时连接B的轻绳上的拉力大小.