如图甲所示,真空中相距为d=6cm的两块平行金属板A、B与某一电源(图中未画)连接,其中B板接地(电势为零),A板的电势随时间的变化规律如图乙所示(U0已知)。将一个质量m、电荷量q的带负电粒子从临B板处无初速度释放,不计粒子重力。求A板电势变化周期T(未知)为多大时,在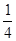 T到
T到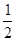 T时刻内,任意时刻释放的该粒子,粒子都不能到达A板(粒子若运动到B板,将被吸附在B板不再运动)。
T时刻内,任意时刻释放的该粒子,粒子都不能到达A板(粒子若运动到B板,将被吸附在B板不再运动)。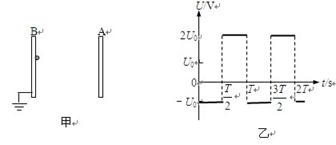
如图甲所示,真空中相距为d=6cm的两块平行金属板A、B与某一电源(图中未画)连接,其中B板接地(电势为零),A板的电势随时间的变化规律如图乙所示(U0已知)。将一个质量m、电荷量q的带负电粒子从临B板处无初速度释放,不计粒子重力。求A板电势变化周期T(未知)为多大时,在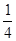 T到
T到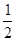 T时刻内,任意时刻释放的该粒子,粒子都不能到达A板(粒子若运动到B板,将被吸附在B板不再运动)。
T时刻内,任意时刻释放的该粒子,粒子都不能到达A板(粒子若运动到B板,将被吸附在B板不再运动)。