飞行时间质谱仪可对气体分子进行分析。如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生电荷量为q、质量为m的正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器。已知a、b板间距为d，极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。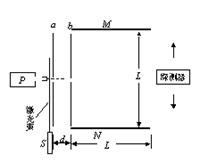
（1）当a、b间的电压为U1，在M、N间加上适当的电压U2，使离子到达探测器。求离子到达探测器的全部飞行时间。
（2）为保证离子不打在极板上，试求U2与U1的关系。
一小石块从空中自由下落h=5m后，掉入淤泥，落到淤泥底时速度恰好为零，全过程共用时t=1.2s．假设石块在淤泥中做匀减速直线运动，且g=10m/s2，则：
（1）小石块掉入淤泥前的瞬时速度v大小为多少；
（2）石块陷入淤泥的深度d及此过程石块的加速度a的大小．
如图所示是一个物体沿直线运动的s﹣t图象．求：
（1）第5秒末的速度大小；
（2）0～60秒内的总路程；
（3）在v﹣t坐标中作出0～60s内物体的速度﹣时间图象．
如图，A、B为两块水平放置的带等量异种电荷的平行金属板，一个质量m=10﹣4kg，电荷量q=5×10﹣5C的带正电粒子静止于两板的正中央，已知两板间距离为20cm，g=10m/s2，求：
（1）两板间匀强电场的场强大小；
（2）两板间的电势差；
（3）若用某种方法将带电粒子的带电荷量减少一半，使带电粒子从两板正中央由静止开始运动，则经过多长时间粒子撞到板上．
如图，真空中xOy平面直角坐标系上的ABC三点构成等边三角形，边长L=2.0m，若将电荷量均为q=+2.0×10﹣6C的两点电荷分别固定在A、B点，已知静电力常量k=9.0×109N•m2/C2，求：
（1）两点电荷间的库仑力大小；
（2）C点的电场强度的大小和方向．
粤公网安备 44130202000953号