做匀变速直线运动的小车带动纸带通过打点计时器,打出的部分计数点如图所示.每相邻两计数点间还有四个点未画出来,打点计时器使用的是50 Hz的低压交流电. (结果均保留两位小数)
①求打点计时器打“2”时,小车的速度v2 = m/s.
②小车的加速度大小为________m/s2(要求用逐差法求加速度)
③请你依据本实验原理推断第7计数点和第8计数点之间的距离大约是 cm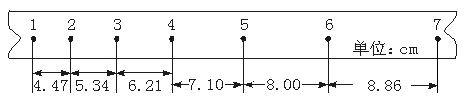
做匀变速直线运动的小车带动纸带通过打点计时器,打出的部分计数点如图所示.每相邻两计数点间还有四个点未画出来,打点计时器使用的是50 Hz的低压交流电. (结果均保留两位小数)
①求打点计时器打“2”时,小车的速度v2 = m/s.
②小车的加速度大小为________m/s2(要求用逐差法求加速度)
③请你依据本实验原理推断第7计数点和第8计数点之间的距离大约是 cm