如图所示，一质量为M＝5 kg的斜面体放在水平地面上，斜面体与地面的动摩擦因数为μ1＝0.5，斜面高度为h＝0.45 m，斜面体与小物块的动摩擦因数为μ2＝0.8，小物块的质量为m＝1kg，起初小物块在斜面的竖直面上的最高点。现在从静止开始在M上作用一水平恒力F，并且同时释放m，取g＝10 m/s2，设小物块与斜面间最大静摩擦力等于它们之间的滑动摩擦力，小物块可视为质点。问：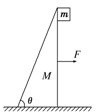
(1)要使M、m保持相对静止一起向右做匀加速运动，加速度至少多大？
(2)此过程中水平恒力至少为多少？
如图甲所示，水平面上有两电阻不计的光滑金属导轨平行固定放置，间距d=0．5m，导轨左端通过导线与阻值为2Ω的电阻R连接，右端通过导线与阻值为4Ω的小灯泡L连接。在矩形区域CDFE内有竖直向上的匀强磁场，CE长为2m，CDFE区域内磁场的磁感应强度B随时间变化的关系如图乙所示，在t=0时，一阻值为2Ω的金属棒在水平恒力F作用下由静止开始从AB位置沿导轨向右运动，在金属棒从AB位置运动到EF位置的过程中，小灯泡的亮度没有发生变化，求：
（1）通过小灯泡的电流大小
（2）恒力F的大小
（3）4s末金属棒的速度大小
（4）金属棒的质量
如甲图所示，水平光滑地面上用两颗钉子（质量忽略不计）固定停放着一辆质量为M=3kg的小车，小车的四分之一圆弧轨道是光滑的，半径为R=0.5m，在最低点B与水平轨道BC相切，视为质点的质量为m=1kg的物块从A点正上方距A点高为h=0.3m处无初速下落，恰好落入小车圆弧轨道滑动，然后沿水平轨道滑行恰好停在轨道末端C。
现去掉钉子（水平面依然光滑未被破坏）不固定小车，而让其左侧靠在竖直墙壁上，该物块仍从原高度处无初速下落，如乙图所示。
不考虑空气阻力和物块落入圆弧轨道时的能量损失，已知物块与水平轨道BC间的动摩擦因数为μ=0.2
求:（1）水平轨道BC长度；
（2）小车固定时物块到达圆弧轨道最低点B时对轨道的压力；
（3）小车不固定时物块再次停在小车上时距小车B点的距离；
（4）两种情况下由于摩擦系统产生的热量之比。
如图所示，单摆摆长为1m，做简谐运动，C点在悬点O的正下方，D点与C相距为2m，C、D之间是光滑水平面，当摆球A到左侧最大位移处时，小球B从D点以某一速度匀速地向C点运动，A、B二球在C点迎面相遇，求小球B的速度大小．（近似取
）
面积S = 0.2m2、n = 100匝的圆形线圈，处在如图所示的磁场内（线圈右边的电路中没有磁场），磁感应强度随时间t变化的规律是B = 0.02t，R = 3Ω，线圈电阻r = 1Ω，求：通过R的电流大小
,金属棒ab可沿导轨滑动，匀强磁场的磁感应强度为B="0.5T," ab在外力作用下以V=5m/s的速度向右匀速滑动，求金属棒所受外力的大小。（金属棒和导轨的电阻不计） 
粤公网安备 44130202000953号