如右图所示,水平放置的两导轨P、Q间的距离L=0.5 m,垂直于导轨平面的竖直向上的匀强磁场的磁感应强度B=2 T,垂直于导轨放置的ab棒的质量m=1 kg,系在ab棒中点的水平绳跨过定滑轮与重量G=3 N的物块相连.已知ab棒与导轨间的动摩擦因数μ=0.2,电源的电动势E=10 V、内阻r=0.1 Ω,导轨的电阻及ab棒的电阻均不计.要想ab棒处于静止状态,R应在哪个范围内取值?(g取10 m/s2)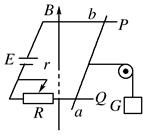
如右图所示,水平放置的两导轨P、Q间的距离L=0.5 m,垂直于导轨平面的竖直向上的匀强磁场的磁感应强度B=2 T,垂直于导轨放置的ab棒的质量m=1 kg,系在ab棒中点的水平绳跨过定滑轮与重量G=3 N的物块相连.已知ab棒与导轨间的动摩擦因数μ=0.2,电源的电动势E=10 V、内阻r=0.1 Ω,导轨的电阻及ab棒的电阻均不计.要想ab棒处于静止状态,R应在哪个范围内取值?(g取10 m/s2)