在真空中,半径为r的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的磁感应强度大小也为B的匀强磁场.一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电荷量q=+5×10-6 C,不计重力,磁感应强度B=1 T,粒子运动速度v0=5×103 m/s,圆形区域半径r=0.2 m,求粒子第一次回到P点所需时间.(结果用π表示)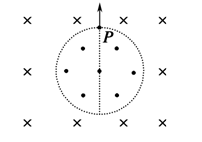
在真空中,半径为r的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的磁感应强度大小也为B的匀强磁场.一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电荷量q=+5×10-6 C,不计重力,磁感应强度B=1 T,粒子运动速度v0=5×103 m/s,圆形区域半径r=0.2 m,求粒子第一次回到P点所需时间.(结果用π表示)