如图所示为一列简谐横波在t=0时刻的图象。此时质点P的运动方向沿y轴负方向且当t=0.55s时质点P恰好第3次到达y轴正方向最大位移处。问: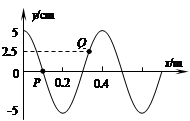
(1)该简谐横波的波速v的大小和方向如何?
(2)从t=0至t=1.2s,质点Q运动的路程L是多少?
(3)当t=1.2s时,质点Q相对于平衡位置的位移s的大小是多少?
如图所示为一列简谐横波在t=0时刻的图象。此时质点P的运动方向沿y轴负方向且当t=0.55s时质点P恰好第3次到达y轴正方向最大位移处。问: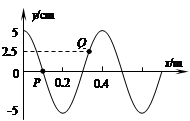
(1)该简谐横波的波速v的大小和方向如何?
(2)从t=0至t=1.2s,质点Q运动的路程L是多少?
(3)当t=1.2s时,质点Q相对于平衡位置的位移s的大小是多少?