(18分)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线y=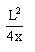 的一段(0≤x≤ L, 0≤y≤ L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,求:
的一段(0≤x≤ L, 0≤y≤ L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,求:
(1)从电场区域Ⅰ的边界B点处由静止释放电子,电子离开MNPQ时的坐标;
(2)由电场区域Ⅰ的AB曲线边界由静止释放电子离开MNPQ的最小动能;
(18分)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线y=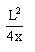 的一段(0≤x≤ L, 0≤y≤ L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,求:
的一段(0≤x≤ L, 0≤y≤ L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,求:
(1)从电场区域Ⅰ的边界B点处由静止释放电子,电子离开MNPQ时的坐标;
(2)由电场区域Ⅰ的AB曲线边界由静止释放电子离开MNPQ的最小动能;