缓冲装置可抽象成如右图所示的简单模型，图中A、B为原长相等、劲度系数分别为k1、k2(k1≠k2)的两个不同的轻质弹簧．下列表述正确的是( )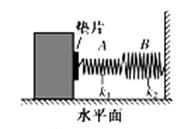
A．装置的缓冲效果与两弹簧的劲度系数无关
B．垫片向右移动稳定后，两弹簧产生的弹力之比F1∶F2＝k1∶k2
C．势片向右移动稳定后，两弹簧的长度之比l1∶l2＝k2∶k1
D．垫片向右移动稳定后，两弹簧的压缩量之比x1∶x2＝k2∶k1
相关试题
同步卫星轨道半径为r，运行速率为v1，加速度为a1；地球赤道上的物体随地球自转的向心加速度为a2；第一宇宙速度为v2；地球半径为R。则下列关系式正确的是（）
A． = |
B．=( )2 |
C． = |
D．= |
一辆空车和一辆满载货物的同型号的汽车，在同一路面上以相同的速度向同一方向行驶．紧急刹车后(即车轮不滚动只滑动)那么 ( )
| A．货车由于惯性大，滑行距离较大 |
| B．货车由于受的摩擦力较大，滑行距离较小 |
| C．两辆车滑行的距离相同 |
| D．两辆车滑行的时间相同 |
粤公网安备 44130202000953号