飞行员驾驶飞机在空中竖直平面内做飞行表演，已知该飞行员身体所能承受的最大加
速度为5g（即重力加速度的5倍），若飞机从高处向下俯冲然后在竖直平面内做匀速圆周
运动，轨迹圆周半径r为2500米，如图所示。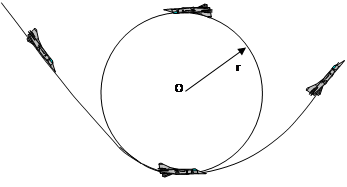
求（1）飞机圆周运动的最大速度；
（2）飞行员在轨道最低点时，飞机对飞行员的作用力是飞行员体重的多少倍。（g=10m/s2）
相关试题
质量为1kg的小球用长为0.5m的细线悬挂在O点，O点距地面高度为1m，如果使小球绕OO′轴在水平面内做圆周运动，若细线受到拉力为12.5N就会被拉断。求：
（1）当小球的角速度为多大时线将断裂？
（2）小球落地点与悬点的水平距离。（g取10 m/s2）
某个质量为m的物体在从静止开始下落的过程中，除了重力之外还受到水平方向的大小、方向都不变的力F=
mg的作用。
（1）这个物体在沿什么样的轨迹运动？求它在时刻t的速度大小。
（2）建立适当的坐标系，写出这个坐标系中代表物体运动轨迹的x、y之间的关系式。
质量为1kg的小球用长为0.5m的细线悬挂在O点，O点距地面高度为1m，如果使小球绕OO′轴在水平面内做圆周运动，若细线受到拉力为12.5N就会被拉断。求：
（1）当小球的角速度为多大时线将断裂？
（2）小球落地点与悬点的水平距离。（g取10 m/s2）
某个质量为m的物体在从静止开始下落的过程中，除了重力之外还受到水平方向的大小、方向都不变的力F=
mg的作用。
（1）这个物体在沿什么样的轨迹运动？求它在时刻t的速度大小。
（2）建立适当的坐标系，写出这个坐标系中代表物体运动轨迹的x、y之间的关系式。
粤公网安备 44130202000953号