如图半径分别为
,
的两圆
和
相交于
,
两点,且点
,两圆同时与两坐标轴相切,
与
轴,
轴分别切于点
,点
,
与x轴,
轴分别切于点
,点
.
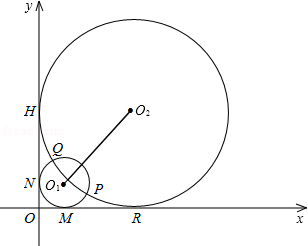
(1)求两圆的圆心
,
所在直线的解析式;
(2)求两圆的圆心
,
之间的距离
;
(3)令四边形
的面积为
,四边形RMO1O2的面积为
.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
相关知识点
推荐套卷
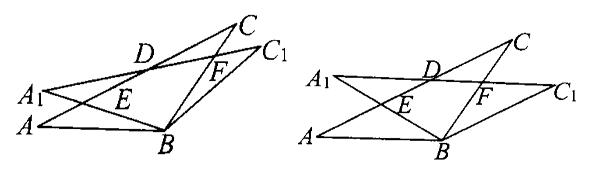
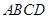 内接于⊙
内接于⊙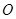 ,
,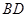 是⊙
是⊙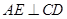 ,垂足为
,垂足为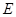 ,
, 平分
平分 .
.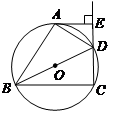
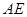 是⊙
是⊙ ,求
,求

 粤公网安备 44130202000953号
粤公网安备 44130202000953号