(1)如图所示,一列简谐横波沿x轴正方向传播,从波传到x="5" m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4 s,下面说法中正确的是()

| A.此列波的频率为2.5 Hz |
| B.若该波传播中遇到宽约3 m的障碍物能发生明显的衍射现象 |
| C.质点Q(x="9" m)经过0.5 s第一次到达波谷 |
| D.质点P在0.1 s内沿波传播方向的位移为1 m |
E. 若在Q(x="9" m)处放一接收器,接到的波的频率小于2.5 Hz
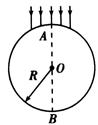
(2)如图所示是一个透明圆柱的横截面,其半径为R,折射率是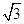 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体. 若一条入射光经折射后恰经过B点,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体. 若一条入射光经折射后恰经过B点,试求:
①这条入射光线到AB的距离是多少?
②这条入射光线在圆柱体中运动的时间是多少?