如图为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为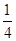 圆周,圆心为O.某单色光线a从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.求 ①该棱镜对单色光线a的折射率n?
圆周,圆心为O.某单色光线a从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.求 ①该棱镜对单色光线a的折射率n?
②改用波长λ更长的单色光线b从AB面入射。入射角
同样为θ1=60°时,判断单色光线b能从BF面射出吗?说出理由.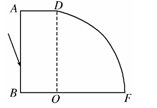
如图为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为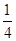 圆周,圆心为O.某单色光线a从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.求 ①该棱镜对单色光线a的折射率n?
圆周,圆心为O.某单色光线a从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.求 ①该棱镜对单色光线a的折射率n?
②改用波长λ更长的单色光线b从AB面入射。入射角
同样为θ1=60°时,判断单色光线b能从BF面射出吗?说出理由.