如图所示,一个人用一根长为0.5 m的细绳拴一个质量为0.5 kg的小球(可视为质点),使其在竖直平面内做圆周运动,若在某一次实验中小球转至最低点时绳子恰好断了,现测得小球落地点与抛出点间的水平距离为4m。已知圆心O离地面h="2.1" m,
(g取9.8m/s2) 求:
(1)绳子断时小球的速度为多大?
(2)若绳子在最低点断时刚好达到它能承受的最大拉力,求此力。 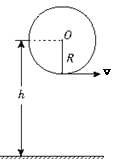
如图所示,一个人用一根长为0.5 m的细绳拴一个质量为0.5 kg的小球(可视为质点),使其在竖直平面内做圆周运动,若在某一次实验中小球转至最低点时绳子恰好断了,现测得小球落地点与抛出点间的水平距离为4m。已知圆心O离地面h="2.1" m,
(g取9.8m/s2) 求:
(1)绳子断时小球的速度为多大?
(2)若绳子在最低点断时刚好达到它能承受的最大拉力,求此力。 