已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.
某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球作圆周运动,由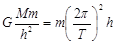 得
得
⑴请判断上面的结果是否正确,并说明理由.如不正确,请给出正确的解法和结果.
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.
某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球作圆周运动,由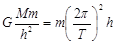 得
得
⑴请判断上面的结果是否正确,并说明理由.如不正确,请给出正确的解法和结果.
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。